영상의 이진화
이진 영상은 화소가 0(흑) 또는 1(백)인 영상으로 주로 영상의 객체 영역과 배경 영역을 구분하기 위해 사용된다.

임계값 T보다 큰 화소는 1, 그렇지 않은 화소는 0으로 바꾸는 과정을 진행하는데, 임계값 T의 결정에 따라 객체 영역과 배경 영역의 구분이 달라진다.
보통은 히스토그램의 계곡 근처 임계값으로 결정해 쏠림 현상을 누그러뜨린다.
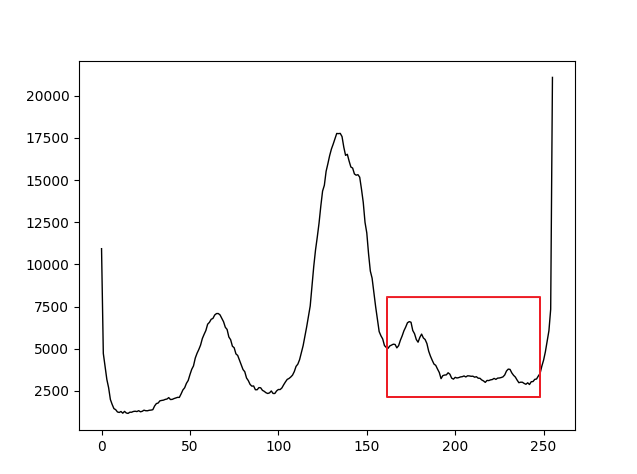
어떤 이미지의 히스토그램을 구한 그래프이다.
그래프에 나타난 것처럼 큰 계곡이 3개, 작은 계곡이 여러 개 임을 확인할 수 있는데,
이처럼 실제 영상에는 계곡이 수 없이 많기 때문에 계곡의 값으로 임계값을 구하는 것은 의미가 없다.
오츄 알고리즘 (Otsu)

오츄는 이진화를 최적화 문제로 바라보았다.
모든 명암값에 대해 목적 함수 J를 구하고 J가 최소인 명암값을 최적값(t)으로 정한다.

J는 0이되는 화소의 분산과, 1이 되는 화소의 분산의 가중치 합으로 J의 값이 작을수록 좋다.
= 분산 값이 작다는 의미로 이미지 내의 픽셀 값들이 얼마나 서로 가까운지를 나타냄
★예시★
[0, 0, 0, 50, 100, 100, 200, 200, 255, 255] 에 대해 임계값 (t = 100) 일 때의 목적 함수 J의 값

클래스 0 (화소가 0) = [0, 0, 0, 50, 100, 100]
클래스 1 (화소가 1) = [200, 200, 255, 255]
μ(평균) 계산
μ0 = 0+0+0+50+100+100 / 6 = 6250 ≈ 41.67
v(분산) 계산

J 계산

오츄는 이런 수식을 반복하면서 J값이 가장 작은 값으로 임계값 t를 정한다.. (= 낱낱 탐색 알고리즘)
낱낱 알고리즘은 시간 복잡도가 크기 때문에 추후에는 탐욕 알고리즘이나 역전파 알고리즘을 사용하여 최적해를 구한다.
모폴로지
영상을 변환하는 과정에서 하나의 물체가 여러 영역으로 분리되거나 다른 물체가 한 영역으로 붙는 경우가 있을 수 있다.
이러한 경우를 보완하기 위해 모폴로지 연산을 수행할 수 있다.
모폴로지는 구조 요소를 이용하여 영역의 모양을 조작한다.
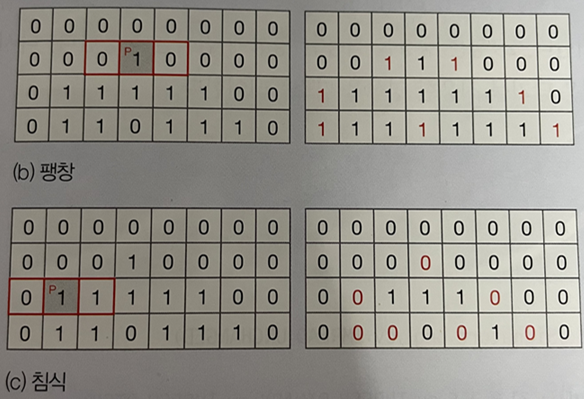
- 팽창
팽창은 구조 요소의 중심을 1인 화소에 씌운 다음 구조 요소에 해당하는 모든 화소를 1로 바꾼다.
- 침식
침식은 구조 요소의 중심을 1인 화소 P에 씌운 다음 구조 요소에 해당하는 모든 화소가 1인 경우에 p를 1로 유지하고,
그렇지 않으면 0으로 바꾼다.
- 열림
침식한 결과에 팽창 연산 수행
- 닫힘
팽창한 결과에 침식 연산 수행

해당 이미지를 팽창, 침식, 닫힘 연산을 수행해 보겠다.
연산을 하기 전에 이 이미지는 [0,0,0] 채널로 이루어진 즉 검은색 이미지다.
이 이미지를 처리하기 위하여 IMREAD_UNCHANGED 인수를 주어 투명값까지 읽어올 수 있도록 설정한다.

마지막 닫힘 이미지의 경우 원본 이미지를 대체한다는 것을 확인할 수 있었다.
점 연산
화소 입장에서 바라본 영상 처리 연산은 화소가 새로운 값을 받는 과정이다.
새로운 값을 어디서 받느냐에 따라 점 연산(자기 자신), 영역 연산(이웃), 기하 연산(다른 곳) 3종류로 구분할 수 있다.
그중 점 연산은 자기 자신으로부터 값을 받는다.
앞에서 공부한 오츄 알고리즘은 점 연산, 모폴로지 연산은 영역 연산에 해당한다!

점 연산은 어두운 사진을 밝게 조절하거나 반대로 밝은 사진을 어둡게 조절할 때 사용한다.
맨 위의 식은 원래의 화소에 a 값을 더해서 밝게 만드는데, 화소가 가질 수 있는 최댓값 L-1을 넘지 않도록 min을 취한다.
반대로 a 값을 빼서 어둡게 만드는 식에는 명암의 최솟값보다 낮아지지 않게 하기 위하여 max를 취한다.

인간의 눈은 빛의 밝기 변화에 비선형적으로 반응한다.
감마 보정은 이런 비선형적인 시각 반응을 수학적으로 표현한다.
이때, f’은 [0, L-1] 범위의 화소 값을 L-1로 나눈 정규값으로 수식을 아래와 같이 수정할 수 있다.
y는 사용자가 조정하는 값으로 y보다 작으면 밝아지고, y보다 크면 어두워진다.

★예시★
[50, 100, 150, 200, 250] 의 이미지에서 y=0.5일 때의 값을 구하라

y보다 작으면 밝아지고, y보다 크면 어두워지는 것을 확인하기 위해 감마 보정을 한 이미지를 확인해 보겠다.


y의 기본값은 1로 설정하고 0.5, 0.75, 1.0, 2.0, 3.0 값을 차례로 확인한 결과 점점 어두워짐을 확인할 수 있었다.
히스토그램 평활화
점 연산은 감마 값에 따라 밝기가 조절되지만
히스토그램 평활화는 히스토그램이 평평하게 되도록 영상을 조작해 영상의 명암 대비를 높인다.
평활화를 하는 이유는 명암 대비가 높아지면서 영상에 있는 물체를 더 잘 식별할 수 있도록 하기 위함이다.

모든 칸의 값을 더하면 1이 되고 0부터 i번칸을 더한 값을 가진 누적 정규화 값을 통해 구할 수 있다.
위 수식을 아래와 같이 풀어쓴다.

★예시★
[2, 12, 17, 10, 3, 7, 11, 2] 값이 주어졌을 때 L=8이므로 최대 밝기 값은 7, 전체 픽셀 수는 64임


히스토그램 평활화 연산을 수행하면 [0, 2, 3, 4, 5, 6, 7, 7]로 평활화되었음을 확인할 수 있다.

평활화 작업 전과 후의 이미지와 히스토그램을 살펴보면
이미지가 좀 더 선명해지고, 화솟값이 100~200 사이에 있는 값만 사용하다가 전체적으로 다 사용함을 확인할 수 있다.
영역 연산 (컨볼루션)
컨볼루션은 입력 영상 f의 각 화소에 필터를 적용해 곱의 합을 구하는 연산으로
이미지의 중요한 특징(에지, 코너, 텍스처 등)을 추출하는 경우 사용한다.

2차원 영상의 컨볼루션에서는 필터 u가 2차원이다.
2차원 필터의 크기를 h x w로 표시하는데 보통 h와 w는 같게 하고, 대칭성을 위해 홀수를 사용한다.
★예시★
아래 3x3 크기의 회색조 이미지와 3x3 크기의 평균 필터(스무딩 필터) u가 있다.


(1,1) 중앙 픽셀에 수식을 적용한다고 할 때,

★예시★
수직 에지 검출 필터를 사용한 예시

(3,2) 위치에 필터를 적용하여 수직 엣지 필터를 사용하였을 때
1x(-1) + 1x0 + 1x3 = 2
1x(-1) + 1x0 + 1x3 = 2
1x(-1) + 1x0 + 1x3 = 2
모두 더하면 6이란 값으로 새로운 픽셀 값을 받는 것을 볼 수 있다.
이때 f'의 그림을 보면 가장자리가 -로 나타난 것을 볼 수 있는데,
이는 필터를 가장자리 화소에 씌우면 필터의 일부가 밖으로 나가기 때문에 적용할 수 없다.
이러한 점을 보완하기 위해 덧대기, 복사 덧대기를 수행할 수 있다.
- 덧대기 : 필요한 만큼 가장자리를 확장한 후 0으로 채움
- 복사 덧대기 : 가장자리 화소의 값으로 채움
위 예시에서 스무딩 필터와 수직 에지 필터를 사용하였다.
이처럼 컨볼루션에는 여러 필터 연산을 수행할 수 있는데 추가로 더 확인해 보겠다.

엠보싱 필터는 물체에 돋음 새김 느낌을 주는 필터이다.
엠보싱 필터 연산을 수행할 때 주의할 점은 오른쪽 아래에서 왼쪽 위를 빼기 때문에 음수 값이 발생할 수 있다.
OpenCV는 주로 명암 단계를 0~255로 표현하며 이를 위해 1바이트를 사용한다.
cv로 읽어온 이미지의 type을 프린트하면 numpy.uint8 값이란 것을 확인할 수 있다.
이때 uint8은 부호 없는 정수의 값만 표현되기에 이 상태에서 엠보싱 필터를 처리하면 의도하지 않은 값이 나올 수 있다.
따라서 np.clip 함수를 이용하여 이 점을 보완한다.
np.clip(a, p, q) 는 a가 p보다 작으면 p, q보다 크면 q로 바꾸고 그렇지 않으면 원본 값을 유지한다.

np.clip을 적용한 것과 적용하지 않은 것, 마지막은 np.clip도 취하지 않고 uint8 값도 취하지 않은 화면이다.
그 외에 에지를 선명하게 해서 물체의 식별을 돕는 샤프닝 필터, 잡음을 제거하는 가우시안 필터가 있다.
샤프닝 필터는 잡음을 유발하고, 가우시안 필터는 과한 블러링 부작용이 있다. 둘이 상반됨!
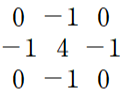

가우시안 필터를 수식화 하면 아래와 같다.

표준편차 σ가 클수록 넓고 완만한 블러 효과를 주고,
표준편차 σ가 작을수록 좁고 날카로운 블러 효과를 준다.
이것도 예시를 들어서 수식을 풀면 바로 이해되겠지만.. 난 이해했고.. 귀찮은 관계로 패스..ㅎ;

오른쪽으로 갈수록 표준 편차 값을 크게 잡아보았다. 표준 편차가 클수록 블러 처리가 강하다는 것을 확인할 수 있다.
기하 연산
기하 연산은 이미지의 크기를 조절하거나, 회전할 때 사용하는 연산으로, 자기의 위치에서 멀리 있는 화소에서 값을 가져와서 사용한다.


동차 좌표는 2차원 점 위치 (x,y)에 1을 추가해 3차원 벡터로 표현한다.
동차 좌표에서는 3개 요소에 같은 값을 곱하면 같은 좌표를 나타낸다.

점 P(1,3)을 (2, -1) 만큼 이동시킨다고 했을 때를 계산해 보자.
일단 점 P를 동차 좌표 (1, 3, 1)로 표현하여 아래와 같이 계산한다.


만약 움직이려는 대상이 점이 아니라 사각형일 경우 모든 점에 대해 이런 식으로 계산하면 된다.

위에 이동 및 회전한 값은 (3.598, 0.232, 1)으로 소수의 값으로 연산되었다.
그러나 화소 위치는 정수로 표현되기 때문에 이럴 경우 문제가 발생한다.
간단한 방법으로 반올림하여 적용하면 되지! 라고 할 수 있는데
이럴 경우 ?와 같이 화소 값을 받지 못하여 검은 구멍처럼 표시되는 경우가 발생할 수 있다.
이러한 현상을 에일리어싱 이라 하고, 이런 점을 보완하는 방법이 안티 에일리어싱 이다.

이 그림은 변환된 화소 (j, i)가 4개 화소에 걸쳐있는 상황이다.
이 상황에서는 보간 방법을 통해 개선할 수 있다.
보간에서는 4개 화소와 걸친 비율에 따라 가중 평균하여 화솟값을 계산한다.
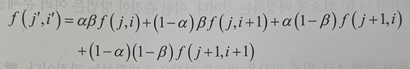
이 수식은 겹치는 비율을 곱하는 방식이기에 선형 보간법에 해당한다.
선형 보간법에는
x, y 두 방향에 걸쳐 계산하는 양선형 보간법,
16개의 이웃과 3차 함수를 사용하는 양3차 보간법이 있다.

cv2를 사용하면 영상 편집 같은 건 쉽게 구현할 수 있기 때문에 이 부분을 다시 공부할 필요가 있을까? 싶었는데
정말 여러 수식을 통해 연산되고 있다는 것을 알게 되었다.
흠.. 이진 처리는 이렇게 공부하면 끝인가..? 아직 뭔가 찜찜하다.. 좀 더 전문적으로 공부해 볼 필요가 있겠군요..
아직 내 거가 되지 않았기 때문에 여러 번 복습해 봐야겠다~
'OpenCV' 카테고리의 다른 글
| [OpenCV] 에지와 영역 분할 (0) | 2025.02.25 |
|---|---|
| [Windows] PyCharm과 Anaconda 설치 및 가상환경 연동하기 (0) | 2025.02.17 |


