에지 검출
에지 검출은 물체 내부의 명암은 서서히 변하고, 외부의 명암은 급격히 변하는 특성을 활용한다.
즉, 객체와 배경이 구분되는 경계선을 찾는다.
에지를 검출하는 이유는 에지를 검출하려는 대상이 사람일 때, 사람의 윤곽 뿐만 아니라 눈, 코, 입을 찾아 추가적인 특징점을 활용하기 위함이다.

미분은 변수 x의 값이 미세하게(델타 x만큼) 증가했을 때 함수의 변화량을 측정한다.

그러나 디지털 영상에서는 연속적인 변화량을 측정할 수 없기 때문에,
위 수식과 같이 픽셀 단위에서 변화량을 구한다.
픽셀의 값이 [10, 15, 20, 18, 12] 라고 주어졌을 때, 미분을 적용하면
f′(1) = f(2) − f(1) =20 − 15 = 5
f′(3) = f(4) − f(3) =12 − 18 = −6
[5, 5, -2, -6]으로 계산된다.
여기서 문제는, 1차 미분을 하면 최대 변화가 일어나는 지점이 에지의 위치와 정확히 일치하지 않을 수 있다는 점이다.
★예시★

픽셀 값이 [10, 10, 10, 100, 100, 100, 100] 라고 주어졌을 때, 밝기가 급격히 변화하는 구간은 3에서 4로 넘어가는 부근이다.
그러나 이 값으로 1차 미분을 진행하게 되면

[0, 0, 90, 0, 0, 0]으로 밝기 변화가 가장 큰 구간을 3이라고 나타낸다.
즉, 1차 미분을 사용하면 영상에서 밝기가 변하는 곳(방향)을 찾을 수 있지만, 정확한 에지의 경계를 찾는 것이 어렵다.
따라서 에지의 정확한 경계를 찾기 위해서 2차 미분을 시도한다. (밝기 변화의 변화량 측정!)

영교차
2차 미분을 적용하면 에지에서 부호가 바뀌는 지점이 발생한다.
이 부분이 정확한 에지를 알려주는 좌표가 된다.

미분을 2번 나눠서 에지의 위치를 구할 수도 있지만 위 그림 처럼 컨볼루션 필터 적용하면 한번에 에지의 위치를 찾을 수 있다.
하지만 이 연산을 통해 구한 값은 2차 미분을 적용한 값이기 때문에 에지의 방향에 대해서는 알 수 없다.
따라서 소벨이나 프리윗 같은 필터를 적용해서 방향성 값을 찾을 수 있다.

해당 수식은 2차원에서 적용할 수 있는 미분 수식으로 x방향과 y방향 두 연산자를 사용한다.

| 프리윗 (Prewitt) | 수직 및 수평 에지 검출 |
| 소벨 (Sobel) | 프레윗 보다 중앙 차이를 더 강조해서 더 강력한 에지 검출 |
방향을 계산하는 공식
| 에지의 강도 | 에지의 방향 |
 |
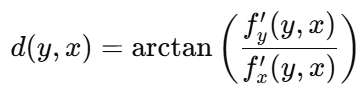 |
| 수평과 수직 방향 미분 결과(위 필터들을 적용한 값)를 이용해 변화량의 크기 계산 | 수직 변화량을 수평 변화량으로 나눈 후 각도를 계산 -> 그 각도가 에지가 향하는 방향을 나타냄 |


소벨 필터를 사용하여 방향을 구하는 예제이다.
그림에 있는 좌표 (3,4)를 대상으로 소벨 필터를 적용하면
f'x = [-3, -2, -1, 0, 0, 0, 3, 6, 3] = 6
f'y = [-3, -6, -3, 0, 0, 0, 1, 2, 3] = -6 값이 나온다.
아크탄젠트를 적용하여 -45도 라는 것을 알 수 있다.
이 때 그레디언트 방향과 에지 방향이 90도로 상반되는 것을 확인할 수 있는데
다시 정리해보자면
에지는 밝기 변화가 있는 "경계"이고, 그레디언트는 밝기가 가장 크게 변화하는 "방향"을 가르킨다!
| 소벨 수평 필터 | 소벨 수직 필터 | 에지 강도 계산 |
 |
 |
 |
소벨 수평 필터는 가로로 선명한 에지를 검출하고,
소벨 수직 필터는 세로로 선명한 에지를 검출하는 것을 확인할 수 있다.
캐니 에지 검출 (Canny)
현실 세계의 이미지에는 노이즈가 상당히 많다.
이 노이즈가 많은 이미지에 소벨 필터를 컴볼루션하게 되면 불필요한 에지(거짓 에지)를 검출할 가능성이 높다.
이러한 문제점을 해소하기 위하여 "진짜" 에지만 남기도록 여러 단계를 거치는 캐니 알고리즘이 나타났다.
비최대 억제(Non-Maximum Suppression)
에지 방향에 수직인 두 이웃 화소의 에지 강도가 자신보다 작으면 에지로 살아남고, 그렇지 않으면 에지가 아닌 화소로 바꾸는 작업이다.
즉, 두 이웃 화소와 비교해 자신이 최대가 아니면 억제된다.
이 작업을 하는 이유는, 두꺼운 에지를 얇게 만들어 에지의 경계선을 더 확실히 하기 위함이다.
이중 임계값 (T low, T high) = 에지 추척
비최대 억제 작업 이후 남아있는 에지들 중에서도 강한 에지는 남기고, 약한 에지(강한 에지와 연관없는)는 제거하는 작업이다.
캐니는 T high 값을 T low의 2~3배로 설정할 것을 권고했다.

임계값을 작게한 이미지는 등번호 3을 잘 인식했지만, 잔디밭에서 많은 잡은 에지가 발생하였고,
임계값을 높게한 이미지는 등번호 3의 획 일부가 손실된 것을 확인할 수 있다.
임계값이 높으면 더욱 확실한(에지 강도가 큰) 화소만 추적하기 때문에 더 적은 에지가 발생한다.
직선 검출
캐니 에지 검출은 검출된 에지의 화소를 1, 에지가 아닌 화소를 0으로 표시한다.
사람의 눈에는 에지가 연결된 선분으로 보이는데 에지 맵에는 연결 관계가 암시적으로 나타나있을 뿐 명시적으로 표현되어 있지 않다.

해당 이미지는 8-연결 요소를 활용하여 에지 화소를 서로 연결하여 경계선을 구성한 예이다. (색깔은 의미없음!)

직선 길이가 50 이상인 경계만 골라서 초록색으로 그림을 그려놓은 이미지이다.
캐니에서는 잔디에 잡음이 많이 검출되었다면, 직선 검출에서는 상당히 개선되었음을 확인할 수 있다.
허프 변환 (Hough Transform)
위 직선 검출에서는 이웃한 에지를 연결하여 경계선을 검출하였기 때문에 에지가 중간에 자잘하게 끊겨 나타날 수 있다.

좌표 (1,3)과 (3,1)를 직선 y=ax+b로 표현하면
b = -a + 3
b = -3a + 1 로 표현할 수 있다.
허프 변환은 이 두 직선이 만나는 지점 (-1, 4)을 투표로 알아낸다.
직선이 지나지 않는 곳은 0, 직선이 지나는 곳은 1표, 두 직선이 만나는 곳은 2표를 받는다.
정리하자면 이들 직선이 만나는 점 (a, b)를 찾아 a를 기울기, b를 y 절편으로 취하고(y=-1x+4) 만나는 점은 투표로 알아낸다.
직선이 만나는 점을 찾기 때문에 끊겼던 곳을 모아모아 선분 또는 원으로 검출하게 된다.
그러나 허프 변환을 실제로 적용할 때는 아래와 같은 문제점이 발생한다.
1. 해상도가 너무 큼 (매우 많은 투표가 생김 = 잡음 까지 검출되는 문제 발생)
2. 기존의 y = ax + b 방정식을 사용하면 수직선인 경우 기울기(a)가 무한대가 되는 문제 발생
이 두 문제를 해결하기 위해 위에서 말한 비최대 억제와 극좌표계 방식을 사용한다.

비최대 억제는 아까 설명했으니 여기선 생략하고,
위 수식에서 ρ (극좌표계 ρ, θ )는 원점 (0,0)에서 직선까지의 수직 거리다.
극좌표계는 기울기 없이 직선을 표현하기 때문에 y = ax + b 같은 수직선도 자연스럽게 표현 가능하다.
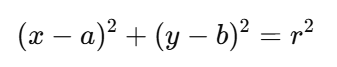
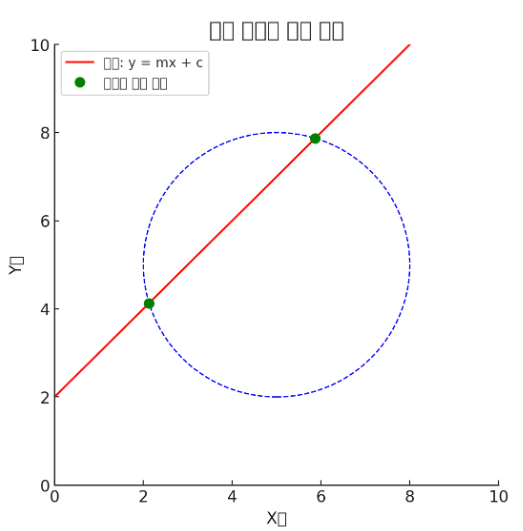

허프 변환으로 직선을 찾으면 직선이 무한히 연장된 형태로 표현되기 때문에 해당 직선의 양 끝점을 구하는 추가 과정이 필요하다.
양끝 점을 찾기 위하여 원의 방정식을 활용하는데, 쉽게 원을 사용해서 직선을 잘라 끝점을 표현한다.
RANSAC

허프 변환은 어떤 선분이 있는지 모르기 때문에 모든 점에 같은 투표 기회를 준다.
인라이어와 아웃라이어 구별 없이 모든 샘플이 동등한 자격으로 오류 계산에 참여하기 때문에 실제에서 벗어난 직선을 찾는다.
RANSAC은 인라이어와 아웃라이어가 섞여 있는 상황에서 인라이어를 찾아 최적 근사하는 기법이다.
랜덤한 두 점을 선택하고, 두 점을 지나는 직선(파란 선)을 계산하는 과정을 반복하는데
아래 그림을 통해 설명해 보겠다.

위 그림에서 임계값 d의 값이 5라면
(a) 1차 시도에서 직선에서 t만큼 떨어진 구간 안에 점이 3개뿐이므로 버림
(b) 2차 시도에서 구간 안에 점 7개가 있으므로 최적 직선으로 추정하고, 추정 오류가 임계값 e보다 작으면 후보군에 추가하고, 그렇지 않으면 버린다.
이런식으로 계속 반복하는 알고리즘으로 반복 횟수가 많을수록 진짜 직선을 찾을 확률이 높아진다.

'OpenCV' 카테고리의 다른 글
| [OpenCV] 이진 영상 처리 (0) | 2025.02.18 |
|---|---|
| [Windows] PyCharm과 Anaconda 설치 및 가상환경 연동하기 (0) | 2025.02.17 |


